|
We have a hyperbolic IFS with three maps, each a similitude of ratio r < 1. Therefore the similarity dimension, d, of the unique invariant set of the IFS is the solution to 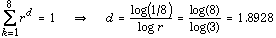 |
|
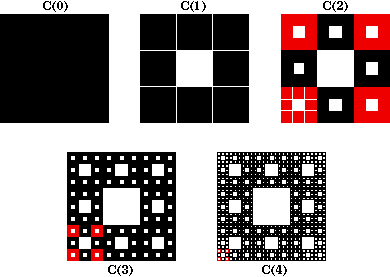
Suppose the area of the original square C(0) is equal to 1. To get C(k+1), we scale C(k) by 1/3, which reduces the area by 1/9 = (1/3)2. But we make 8 copies of this scaled version to form C(k+1). Therefore the area of C(k+1) must be (8/9)th of the area of C(k). This means that the area of C(n) is (8/9)n for all n. Notice that these areas go to 0 as n goes to infinity. This means that we have removed "all" of the area of the original square in constructing the Sierpinski carpet. But of course there are many points still left in the carpet. That is one reason why area is not a useful dimension for this set.
Sierpinski used the carpet to catalogue all compact one-dimensional objects in the plane (from a topological point of view). What this basically means is the Sierpinski carpet contains a topologically equivalent copy of any compact one-dimensional object in the plane. Thus for any curve contained in the plane, there is a set homeomorphic to the Sierpinski carpet that contains the curve. For a good discussion of this idea, consult the text by Peitgen, Jurgens, and Saupe [6], or the topology text by Engelking and Sieklucki [2].
In an article written in 1916, Sierpinski wrote [1]:
Note that as early as one year ago Mr. Mazurkiewicz found an example of a curve which was simultaneously a Jordan curve and a Cantor curve...Mazurkiewicz forms this curve by dividing the square into nine smaller squares using lines parallel to the sides and removing the interior of the center square, performing the same procedure on each of the remaining eight square, and iterating this procedure ad infinitum. So the Sierpinski carpet was actually invented by Stefan Mazurkiewicz, who in 1913 wrote his Ph.D. thesis under the supervision of Sierpinski on curves filling a square. For an example of how the Sierpinski Carpet has been an artistic inspiration, see the picture of the quilt "Sierpinksi Meets Mondrian" designed by Professor Gerda de Vries, University of Alberta.
|
|
|
|
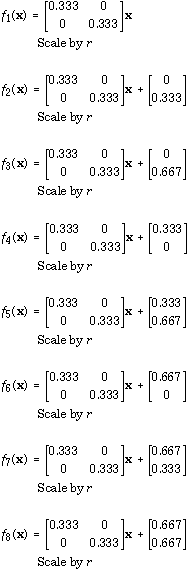
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου