This project models the rebellion of a subjugated population against a central authority. It is is an adaptation of Joshua Epstein's model of civil violence (2002). http://ccl.northwestern.edu/netlogo/
Kehagiat Sci
Δευτέρα 27 Ιουνίου 2011
NetLogo Rebellion!!!
This project models the rebellion of a subjugated population against a central authority. It is is an adaptation of Joshua Epstein's model of civil violence (2002). http://ccl.northwestern.edu/netlogo/
Δευτέρα 20 Ιουνίου 2011
Boids!!!
http://www.red3d.com/cwr/boids/
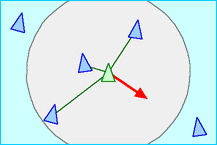
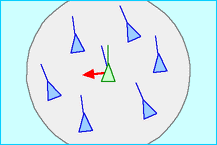
In 1986 I made a computer model of coordinated animal motion such as bird flocks and fish schools. It was based on three dimensional computational geometry of the sort normally used in computer animation or computer aided design. I called the generic simulated flocking creatures boids. The basic flocking model consists of three simple steering behaviors which describe how an individual boid maneuvers based on the positions and velocities its nearby flockmates:
Each boid has direct access to the whole scene's geometric description, but flocking requires that it reacts only to flockmates within a certain small neighborhood around itself. The neighborhood is characterized by a distance (measured from the center of the boid) and an angle, measured from the boid's direction of flight. Flockmates outside this local neighborhood are ignored. The neighborhood could be considered a model of limited perception (as by fish in murky water) but it is probably more correct to think of it as defining the region in which flockmates influence a boids steering.
In 1986 I made a computer model of coordinated animal motion such as bird flocks and fish schools. It was based on three dimensional computational geometry of the sort normally used in computer animation or computer aided design. I called the generic simulated flocking creatures boids. The basic flocking model consists of three simple steering behaviors which describe how an individual boid maneuvers based on the positions and velocities its nearby flockmates:
 | Separation: steer to avoid crowding local flockmates | |
 | Alignment: steer towards the average heading of local flockmates | |
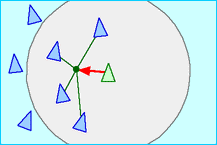 | Cohesion: steer to move toward the average position of local flockmates |
Τρίτη 14 Ιουνίου 2011
Cellular Automaton Traffic Simulators
This applet demonstrates the simulation of traffic flow by cellular automata. You get pictures like this:
There is a great theory on cellular automata as traffic models. You can read about it (for example) here or here.
Are you interested in cellular automata generally? They can produce great pictures:
If you want to know the theory behind the pictures, read this.
Δευτέρα 13 Ιουνίου 2011
Sierpinski Carpet
(http://ecademy.agnesscott.edu/~lriddle/ifs/carpet/carpet.htm)
Start with a solid (filled) square C(0). Divide this into 9 smaller congruent squares. Remove the interior of the center square (that is, do not remove the boundary) to get C(1). Now subdivide each of the eight remaining solid squares into 9 congruent squares and remove the center square from each to obtain C(2). Continue to repeat the construction to obtain a decreasing sequence of sets 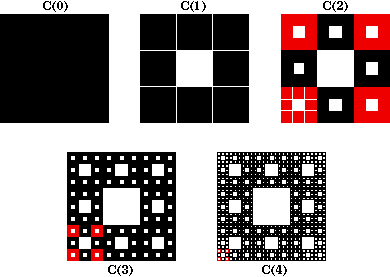 | ||||||
| ||||||
| ||||||
Σάββατο 11 Ιουνίου 2011
Self referential sentences
From http://www.lboro.ac.uk/departments/ma/gallery/selfref/index.html.
Produced by Andy Burbanks The following is adapted from an idea presented by Douglas Hofstadter in his wonderful book Metamagical Themas. A very peculiar sentence...Can you see anything special about the following sentence?In this sentence, the number of occurences of 0 is 1, of 1 is 11, of 2 is 2, of 3 is 1, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 1, of 8 is 1, and of 9 is 1.This is, in fact, a self-referential self-documenting sentence. By self-referential, we mean that it talks about itself. By self-documenting we mean that it makes a (true) statement about its own contents. In this case, it makes a true statement about the number of occurences of each of the digits 0 to 9 that it contains It is very important that the statement it makes is true, because there are plenty of statements of this kind that are false. Just try putting a few randomly chosen numbers into the sentence instead: it is highly unlikely that you will get a true statement just by chance! You might think that the above statement is perhaps unique, but it's not the only one! The following sentence has the same property. In this sentence, the number of occurences of 0 is 1, of 1 is 7, of 2 is 3, of 3 is 2, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 2, of 8 is 1, and of 9 is 1. Stranger still...There is at least one creature that is weirder than the above: What about the following pair of sentences?In the next sentence, the number of occurences of 0 is 1, of 1 is 7, of 2 is 4, of 3 is 1, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 1, of 8 is 2, and of 9 is 1. In the previous sentence, the number of occurences of 0 is 1, of 1 is 8, of 2 is 2, of 3 is 1, of 4 is 2, of 5 is 1, of 6 is 1, of 7 is 2, of 8 is 1, and of 9 is 1.These take a peculiar interest in each others contents! But what is more interesting is that both of the sentences are true simultaneously. That is, each of the sentences makes a true statement about the other. ConstructionHow is it possible to come up with these strangely introspective sentences?Firstly, consider the blank `template sentence': In this sentence, the number of occurences of 0 is _, of 1 is _, of 2 is _, of 3 is _, of 4 is _, of 5 is _, of 6 is _, of 7 is _, of 8 is _, and of 9 is _.What is needed is some way of filling in the gaps. Choosing an initial valueSuppose that we begin by putting in any ten numbers, even though the resulting sentence is almost bound to be false. Each choice of ten numbers gives a vector of ten entries. For example, choosing all of the numbers to be zero gives the vector:(0,0,0,0,0,0,0,0,0,0)The corresponding sentence would be: In this sentence, the number of occurences of 0 is 0, of 1 is 0, of 2 is 0, of 3 is 0, of 4 is 0, of 5 is 0, of 6 is 0, of 7 is 0, of 8 is 0, and of 9 is 0.In this case, the sentence is certainly false since each digit occurs at least once! Applying a processWhat happens if we start with the initial vector chosen above, and then count up the proper numbers of digits that really occur in the corresponding sentence. This gives the new vector:(11,1,1,1,1,1,1,1,1,1)Unfortunately, applying this process has again resulted in a false sentence: In this sentence, the number of occurences of 0 is 11, of 1 is 1, of 2 is 1, of 3 is 1, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 1, of 8 is 1, and of 9 is 1. Iteration and fixed pointsWhat happens if we repeat this process with the new sentence again and again? This is known as iterating the process. Here are the vectors that result:(11,1,1,1,1,1,1,1,1,1)
(1,12,1,1,1,1,1,1,1,1)
(1,11,2,1,1,1,1,1,1,1)
(1,11,2,1,1,1,1,1,1,1)
...
After a few steps, the numbers are no longer changing. The resulting vector(1,11,2,1,1,1,1,1,1,1)is called a fixed-point of the process, since its value does not change when the process is applied. (We might also call it a 1-cycle, i.e. a cycle which repeats every 1 step of the process.) What's more, the corresponding sentence is actually true (in fact, it is the first of the self-documenting sentences given above). 'Attraction' to a fixed pointTrying other initial vectors tends to eventually lead to the same result. This means that the fixed point vector is (in some sense) attracting other vectors to it when the process is applied.Notice how an apparently difficult problem (namely, coming up with correct values to place into the template) has been solved by iterating a simple process. In this case it worked because the fixed point was `attracting' other values when the process was iterated. In fact, the above fixed point is not the only one, there is another (corresponding to the second self-documenting sentence shown above) as can be seen from the following sequence of vectors: (243000,645,9,2225,234,0,23445987,23434,2,34)
(5,1,9,7,9,4,2,2,2,3)
(1,2,4,2,2,2,1,2,1,3)
(1,4,6,2,2,1,1,1,1,1)
(1,7,3,1,2,1,2,1,1,1)
(1,7,3,2,1,1,1,2,1,1)
(1,7,3,2,1,1,1,2,1,1)
...
Cycles (periodic orbits)For some initial vectors, the process does not lead to a fixed point, but instead gives an alternating pair of values. For example:(243,645,9765,2225,2340,300,234,23434,2,34)
(4,1,9,8,8,4,3,2,1,2)
(1,3,3,2,3,1,1,1,3,2)
(1,5,3,5,1,1,1,1,1,1)
(1,8,1,2,1,3,1,1,1,1)
(1,8,2,2,1,1,1,1,2,1)
(1,7,4,1,1,1,1,1,2,1)
(1,8,2,1,2,1,1,2,1,1)
(1,7,4,1,1,1,1,1,2,1)
(1,8,2,1,2,1,1,2,1,1)
...
This is a 2-cycle, i.e. a cycle which repeats every 2 steps. The sequences of values produced by iterating a process is called the orbit of the initial value under the process. Cycles are also called periodic orbits, and a 2-cycle is also known as a periodic orbit having period 2.Notice that the existence of a period-2 orbit implies the existence of a pair of sentences, each of which documents the contents of the other! (These values were used in the self-documenting pair given earlier.) And, in general, if the method were to lead to an N-cycle (for some positive whole number N), then there must be a succession of N sentences, where each one documents the contents of the next (with the final sentence documenting the contents of the first). Other links of interestTo see other examples of iteration leading to fixed points and periodic orbits, see the following sections of the gallery: |
Εγγραφή σε:
Αναρτήσεις (Atom)